This post was written by Dean Markwick, who has put together an excellent example using QuestDB as a time series database for high-frequency trading. This post shows how to use QuestDB to calculate the limit order book, price impact, trade sign distribution, and other concepts via the Julia programming language.
Originally published at Dean's personal blog.
Connecting to QuestDB from Julia lang
In my first post, I showed how to set up a producer/consumer model to build a
BTCUSD trades database using the CoinbasePro WebSocket feed. Now I'll show you
how you can connect to the same database to pull out the data, use some specific
timeseries database queries and hopefully show where this type of database is
helpful by improving some of my old calculations.
I ingested just over 24 hours worth of data over the 24th and 25th of July, 2021, but I completely missed the massive rally, which is just my luck. That would have been interesting to look at, but never mind! I'm going to repeat some of the calculations from older blog posts on high-frequency finance using more data this time.
Julia can connect to the database using the LibPQ.jl package and execute queries using all their functions. This is very handy as we don't have to worry about database drivers or connection methods; we can just connect and go.
using LibPQ
using DataFrames, DataFramesMeta
using Plots
using Statistics, StatsBase
using CategoricalArrays
The following is the default connection credentials for the database used to connect to QuestDB:
conn = LibPQ.Connection("""
dbname=qdb
host=127.0.0.1
password=quest
port=8812
user=admin""")
PostgreSQL connection (CONNECTION_OK) with parameters:
user = admin
password = ********************
dbname = qdb
host = 127.0.0.1
port = 8812
client_encoding = UTF8
options = -c DateStyle=ISO,YMD -c IntervalStyle=iso_8601 -c TimeZone=UTC
application_name = LibPQ.jl
sslmode = prefer
sslcompression = 0
gssencmode = disable
krbsrvname = postgres
target_session_attrs = any
It's very easy; Julia thinks that it is a regular Postgres database. We can quickly move on to working with the data. I started with getting all trades out of the database:
@time trades = execute(conn, "SELECT * FROM coinbase_trades") |> DataFrame
dropmissing!(trades);
nrow(trades)
It takes about 5 seconds to pull 210,000 rows into the notebook:
4.828067 seconds (9.25 M allocations: 335.378 MiB, 1.64% gc time)
Now we can plot the results and export as a .webp:
plot(trades.timestamp, trades.price, label=:none, fmt=:png)
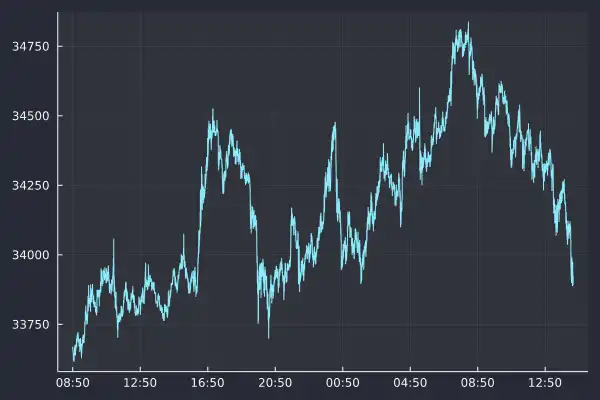
You can see that Plots.jl struggles a little with formatting the x-axis
correctly with a time series plot above. The timestamps are pretty long labels
which could be better if the text was angled 45 degrees. It's a shame that I
missed the sudden rally on Sunday 25th; that was pretty unlucky, but let's move
on to updating previous graphs with the new dataset.
Order sign correlation
The correlation between buys and sells follows a power law. Last time, I only had 1000 trades to work on after pulling them using the REST API. Now I've got 200x more, which should improve the uncertainty around the previous values.
ac = autocor(trades.side)
acplot = plot(1:length(ac), ac, seriestype=:scatter, label = :none, xlab="Lag", ylab = "Correlation")
aclogplot = plot(log.(1:length(ac)), log.(ac), seriestype=:scatter, label=:none, xlab= "log(Lag)", ylab="log(Correlation)")
plot(acplot, aclogplot, fmt=:png)
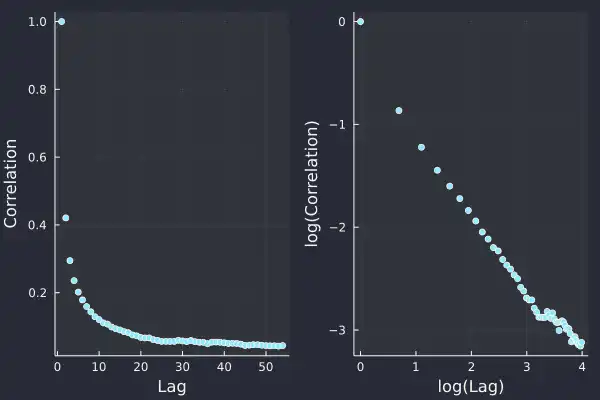
In the log-log plot, we can see a nice straight line which we fit a linear model on.
using GLM
sideModel = lm(@formula(log(AC) ~ log(Lag)), DataFrame(AC=ac, Lag=1:length(ac)))
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}}
:(log(AC)) ~ 1 + :(log(Lag))
Coefficients:
──────────────────────────────────────�────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
──────────────────────────────────────────────────────────────────────────
(Intercept) -0.439012 0.049596 -8.85 <1e-11 -0.538534 -0.339491
log(Lag) -0.70571 0.0156489 -45.10 <1e-42 -0.737112 -0.674308
──────────────────────────────────────────────────────────────────────────
This time we've got a 𝛾 value of 0.7 with more certainty.
plot(log.(1:length(ac)), log.(ac), seriestype=:scatter, label=:none)
plot!(log.(1:length(ac)), coef(sideModel)[1] .+ coef(sideModel)[2] .* log.(1:length(ac)),
label="Model", xlab= "log(Lag)", ylab="log(Correlation)", fmt=:png)
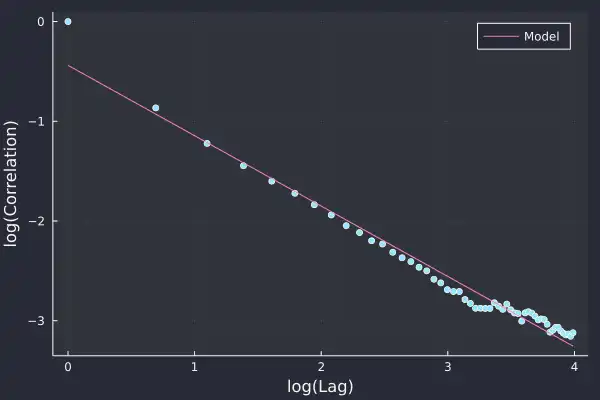
This lines up nicely with the data and is better than the previous attempt with just 1000 trades. 𝛾 is less than one, which means it is a 'long memory' process, so trades in the past affect trades in the future for a long time. This is usually explained as the effect of people breaking up large trades into slices and executing them bit by bit.
Size distribution
Again, the size of each trade follows a power-law distribution too. We use a slightly different method to estimate the exponent, and last time, with just 1000 trades, we struggled to get a stable value. Now, with so much more data, we can have another crack.
uSizes = minimum(trades.size):0.05:maximum(trades.size)
empF = ecdf(trades.size)
tradesSizePlot = plot((uSizes), (1 .- empF(uSizes)), seriestype=:scatter, label="P(V > x)", xlabel="Trade Size", ylabel="Probability")
tradesSizeLogPlot = plot(log.(uSizes), log.(1 .- empF(uSizes)), seriestype=:scatter, label="P(V > x)", xlabel = "log(Trade Size)", ylabel="log(Probability)")
plot(tradesSizePlot, tradesSizeLogPlot, fmt=:png)
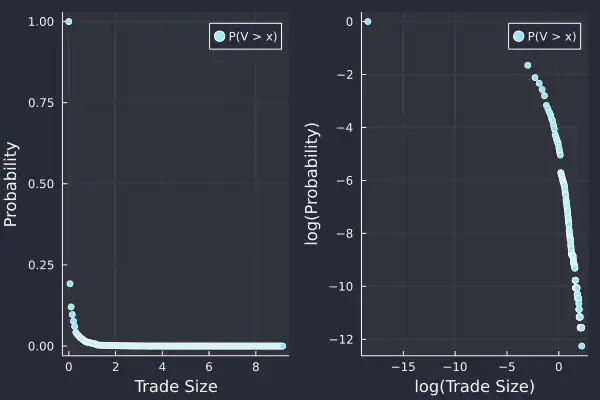
Let's use the same Hill estimator as last time:
function hill_estimator(sizes_sort, k)
N = length(sizes_sort)
res = log.(sizes_sort[(N-k+1):N] / sizes_sort[N-k])
k*(1/sum(res))
end
sizes = trades.size
sizes_sort = sort(sizes)
bds = 2:100:(length(sizes)-1000-1)
alphak = [hill_estimator(sizes_sort, k) for k in bds]
plot(bds, alphak, xlabel="k", ylabel="Alpha", label=:none, fmt=:png)
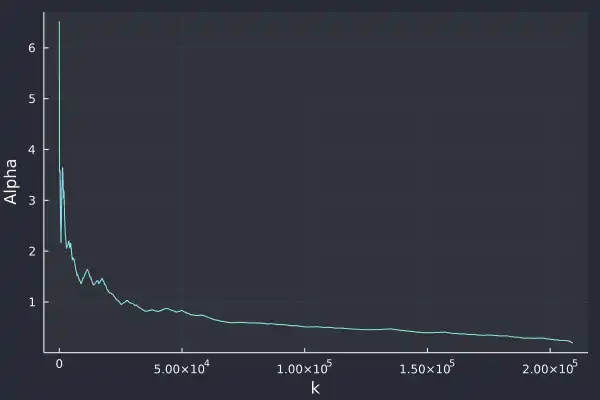
It's still hard to judge whether it is converging to a value or not. It always appears to be decreasing no matter the sample size. Maybe I still need more data, or perhaps I need a better understanding of the Hill estimator!
Market impact
I've not been using QuestDB to its full potential, and repeating all my previous graphs hasn't fully exploited the available features. One of those features is the ability to group by the timestamp across a bucket size (1 second, 5 minutes, etc.) and aggregate the data. We will use that to try and come up with a better model of a market impact than I had in my previous post.
We aggregate the trades into 1-minute buckets and calculate the total volume traded, the total signed volume (sell trades count as negative), the last price and also the number of trades in each bucket.
@time marketimpact = execute(conn,
"SELECT timestamp, sum(size) as TotalVolume,
sum(size*side) as SignedVolume,
last(price) as Close,
count(*) as NTrades
FROM coinbase_trades
SAMPLE by 1m") |> DataFrame
dropmissing!(marketimpact)
marketimpact[1:3, :]
This took less than a second and is a really easy line of code to write:
0.223987 seconds (167.29 k allocations: 8.708 MiB, 56.20% compilation time)
| timestamp | TotalVolume | SignedVolume | Close | NTrades |
|---|---|---|---|---|
| DateTim… | Float64 | Float64 | Float64 | Int64 |
| 2021-07-24T08:50:34.365 | 1.75836 | -0.331599 | 33649.0 | 52 |
| 2021-07-24T08:51:34.365 | 4.18169 | -3.01704 | 33625.2 | 67 |
| 2021-07-24T08:52:34.365 | 0.572115 | -0.325788 | 33620.1 | 46 |
Now for the market impact calculation, we calculated the return bucket to bucket and normalise the signed volume by the total volume traded to give a value of between -1 and 1. This is taken from https://arxiv.org/pdf/1206.0682.pdf and equation 26.
marketimpact[!, :returns] .= 1e4.*[NaN; diff(log.(marketimpact.Close))]
marketimpact[!, :NormVolume] .= marketimpact[!, :SignedVolume] ./ marketimpact[!, :TotalVolume]
miModel = lm(@formula(returns ~ NormVolume + 0), marketimpact[2:end, :])
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}}
returns ~ 0 + NormVolume
Coefficients:
──────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
──────────────────────────────────────────────────────────────────────
NormVolume 4.55478 0.290869 15.66 <1e-51 3.9843 5.12526
──────────────────────────────────────────────────────────────────────
Here we can see that there is a positive coefficient, θ in the paper, as expected, and we can interpret this at how much the price moves after buying or selling. Specifically, in these minute buckets, those that contained only buy trades moved the market up by 4.5bps and the same for sells in the opposite direction.
plot(marketimpact.NormVolume, marketimpact.returns, seriestype=:scatter, label=:none,
xlab="Normalised Volume", ylab="Market Impact (log(bps))")
plot!(-1:0.1:1, coef(miModel)[1] .* collect(-1:0.1:1), label="Model", linewidth=3, legend=:topleft, fmt=:png)
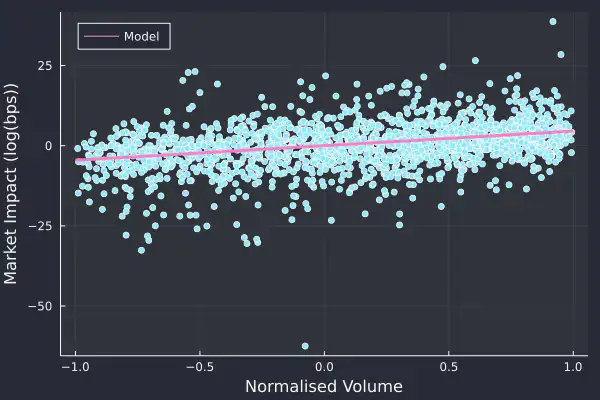
You can see how the model lines of with the data, and there is a very slight trend that is picked. So overall, a better, if still a very simple model of market impact.
Trades with top of book
I've saved down the best bid and offer using the same process as Part 1 of this series. Over the same period, the best bid and offer data has 17 million rows; quite a bit more. I use this best bid-offer data to do an ASOF join. ASOF joins take two tables and joins them such that the timestamps align or the previous observation is used. In our case, we can take the trades, join it with the best bid and best offer table to get where the mid-price was at the time of the trade.
@time trades2 = execute(conn, "SELECT * FROM coinbase_trades ASOF JOIN coinbase_bbo") |> DataFrame
dropmissing!(trades2);
9.745210 seconds (18.49 M allocations: 671.544 MiB, 1.84% gc time)
This took 11 seconds but was all done in the database, so no issue with blowing
out the memory after pulling it into your Julia session. Doing a regular join in
Julia would only match timestamps exactly, whereas we want the last observed
bid/offer price at least making the ASOF function very useful.
We now calculate a mid-price, how far the traded price was from the mid-price, and add an indicator for what quantile the trade size landed. We then group by this quantile indicator and calculate the average trade size and the average distance from the mid-price.
trades2[!, :Mid] .= (trades2.bid .+ trades2.ask)./2;
trades2[!, :Cost] .= 1e4 .* trades2.side .* ((trades2.price .- trades2.Mid) ./ (trades2.Mid))
trades2[!, :SizeBucket] .= cut(trades2[!, :size], [quantile(trades2[!, :size], 0:0.1:1); Inf])
gdata = groupby(@where(trades2, :Cost .> 0), :SizeBucket)
costData = @combine(gdata, MeanSize = mean(:size), MeanCost = mean(:Cost))
logCostPlot = plot(log.(costData.MeanSize),
log.(costData.MeanCost), seriestype=:scatter,
label=:none,
xlab="log(Size)",
ylab="log(Cost)", fmt=:png)
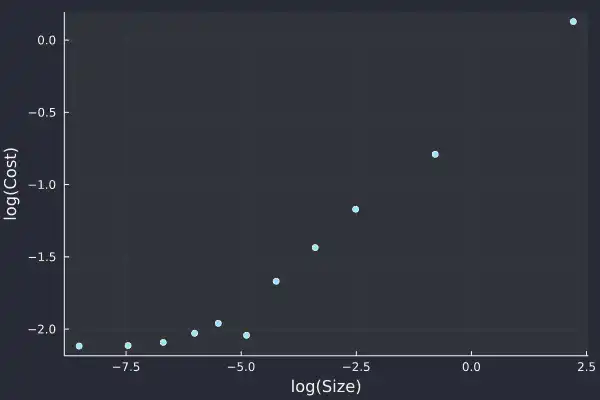
Unsurprisingly, we can see that larger trades are further away from the mid-price when they execute. This is because they are eating through the posted liquidity.
This is very similar to my https://cryptoliquiditymetrics.com/ sweep the book graph, which is estimating the cost of eating liquidity. The graph above shows the actual cost of eating liquidity for real trades that have happened on Coinbase.
We can fit a model to this plot, and it is commonly referred to as the square root law of market impact. We ignore the smaller trade sizes, as they aren't following the nice linear log-log plot.
costModel = lm(@formula(log(MeanCost) ~ log(MeanSize)),
@where(costData, :MeanSize .> exp(-7)))
StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}}
:(log(MeanCost)) ~ 1 + :(log(MeanSize))
Coefficients:
───────────────────────────────────────────────────────────────────────────
Coef. Std. Error t Pr(>|t|) Lower 95% Upper 95%
───────────────────────────────────────────────────────────────────────────
(Intercept) -0.534863 0.0683721 -7.82 0.0001 -0.696537 -0.373189
log(MeanSize) 0.259424 0.0154468 16.79 <1e-06 0.222898 0.29595
───────────────────────────────────────────────────────────────────────────
The 𝛾 value of 0.25 is pretty low compared to other assets, which we would expect to be around 0.5. But we haven't included the usual volatility calculation, which is in front of the volume component.
plot(log.(costData.MeanSize),
log.(costData.MeanCost), seriestype=:scatter,
label=:none,
xlab="log(Size)",
ylab="log(Cost)")
plot!(-8:0.1:3, coef(costModel)[1] .+ coef(costModel)[2] .* (-8:0.1:3),
label="Model", legend=:topleft, fmt=:png)
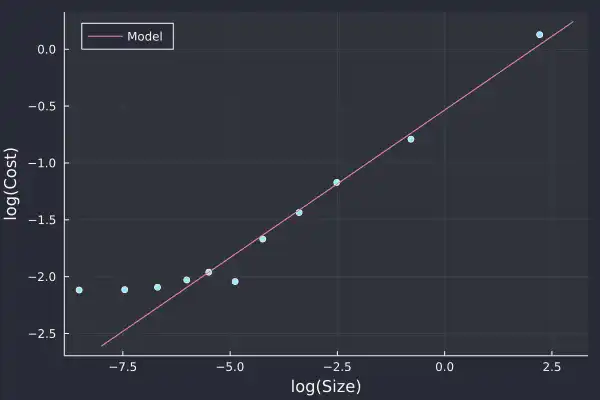
Apart from the small trades, the model lines up well with the increasing trade size.
Using this model, you can start to estimate how much a strategy might cost to implement. The outcome of your strategy is unknown, but your trading costs are known. If it costs you 1bp to enter and exit a trade (round trip), but you only think the price will change by 0.5bps, then you're at a loss even if you were 100% right on the price direction!
Summary
QuestDB makes working with this data incredibly easy. Both aggregating the data
using SAMPLE BY and joining two datasets using AS OF. Connecting to the
database is a doddle using LibPQ.jl, so you can get up and running without any
issues. These things rarely happen straight out of the box.
Using this data, I've ramped up the sample sizes, and all my plots and models look better. Again, all free data and with hopefully, very minimal technical difficulty. As someone that usually finds themselves drowning in CSVs, QuestDB has shown how much more efficient things can be when you use a database.
If you have have feedback or questions about this article, feel free ask in our Community Forum or browse the project on GitHub where we welcome contributions of all kinds.