1BRC merykitty’s Magic SWAR: 8 Lines of Code Explained in 3,000 Words

In a recent blog post I described the most important optimizations I and other contestants applied at the recent One Billion Row Challenge (1BRC). Using them I showed how the performance of the initial idiomatic, parallelized Java code improves by a factor of 40. We went from 71 seconds, down to 1.7.

The optimization techniques we applied ranged from simple and digestible to arcane and mystifying. One technique in particular stood out as especially awesome but cryptic, and I noted that explaining it would take another full blog post.

So, here we are!

Enter the 1BRC

Several experts predicted at the outset of the 1BRC contest that, once the "usual suspects" are dealt with, one particular concern would become the botteneck: parsing the temperature from the CSV file. It isn't a complicated format – the temperature can range from -99.9 to 99.9, so there are a total of four possible arrangements of characters: -XX.X, -X.X, X.X, and XX.X. But, when your goal is to parse one billion of them in less than a second, every little detail and variation becomes an issue.

Initially, contestants used the Double.parseDouble() library call. But soon enough, custom solutions started popping up that were up to a screenful long. Many adopted an approach that looked pretty optimal. It didn't involve any loops, and had the seeming "theoretical minimum" of two branching points, covering the four possibilities.

Then, out of the blue, a solution appeared that set the Twitter #1BRC hashtag on fire. No if statements, and just a single read from the file! It was a part of the solution contributed by Quân Anh Mai (GitHub handle @merykitty). The code looked like nothing less than magic incantations, and even the top experts nodded in disbelief.

Since 1BRC was an open source contest, everyone could look at and copy ideas from others. As a result, this snippet spread like wildfire and became a standard element of all the top solutions. The winning contestant, Thomas Wuerthinger, went as far as listing Quân Anh as a part of the team that contributed to his solution.

Big thanks to Quân Anh, who reviewed this post for correctness and approved it!

Unpacking merykitty’s Magic SWAR

Merykitty's code consists of nothing but a fixed sequence of 18 ALU operations: bitwise shift, AND, NOT and XOR; arithmetic add, subtract, and multiply; and a single low-level function call numberOfTrailingZeros(), for which the JDK has a compiler intrinsic using specialized CPU instructions.

In goes a long number filled with 8 bytes from the CSV (in little-endian order), and out comes the temperature as an integer (10x the actual temperature).

We pack eight bytes of input into a single CPU register, and then perform operations on the register as a whole. Usually, such work is performed using specialized CPU instructions, designed specifically to operate on many bytes of data at once. Such instructions are called "Single Instruction, Multiple Data", or SIMD for short. In this case, we're using standard CPU registers and instructions – this kind of technique goes by the name of "SIMD Within A Register", or SWAR.

The full code at a glance:

private static final long MAGIC_MULTIPLIER = (100 * 0x1000000 + 10 * 0x10000 + 1);
private static final long DOT_DETECTOR = 0x10101000;
private static final long ASCII_TO_DIGIT_MASK = 0x0F000F0F00L;

private static int parseDataPoint(long inputData) {
    long negatedInput = ~inputData;
    long broadcastSign = (negatedInput << 59) >> 63;
    long maskToRemoveSign = ~(broadcastSign & 0xFF);
    long withSignRemoved = inputData & maskToRemoveSign;
    int dotPos = Long.numberOfTrailingZeros(negatedInput & DOT_DETECTOR);
    long alignedToTemplate = withSignRemoved << (28 - dotPos);
    long digits = alignedToTemplate & ASCII_TO_DIGIT_MASK;
    long absValue = ((digits * MAGIC_MULTIPLIER) >>> 32) & 0x3FF;
    long temperature = (absValue ^ broadcastSign) - broadcastSign;
    long nextLineStart = (dotPos >>> 3) + 3;
    return (int) temperature;
}

Note: this is not the exact original code by merykitty. It is slightly transformed for easier reading. View the original.

The value of the inputData parameter comes from a direct native memory read of the mmap'd CSV file. We don't have to deal with that code since it's a separate concern.

Now, we've all seen a line or two of bit-twiddling code here and there that looks cryptic at first. However, after half an hour explaining it to yourself, it becomes kind of familiar and not that scary.

But have you ever seen this much of it in one place? And solving such a complex, high-level problem like parsing temperature? It seems to lie beyond human comprehension.

I'm here to show you that you can get it. It's just a number of steps, after all. They are put together amazingly tight, like a rocket engine. But when you zoom in on each part alone, you'll see it boils down to familiar concepts. No maths beyond 6th grade, I promise!

At a high-level, the code code takes these steps:

1. Detect whether the number is negative (i.e., the first character is -)
2. Zero out the sign character, if any
3. Find where is the decimal dot
4. Shift the contents so that the digits align with the template XY.Z placed over the bits of the long value
5. Transform the ASCII characters to their digit values
6. Multiply each digit by its weight (1x, 10x, 100x), and add them all up
7. Apply the sign

When you break it down into steps like this, it sounds less magical right away. These are the reasonable steps to take. But the really interesting bits come when you try to do them with nothing but ALU operations.

1. Detect the minus sign

This code detects the minus sign:

long negatedInput = ~inputData;
long broadcastSign = (negatedInput << 59) >> 63;

Let me reverse the order of negation (~) and shifting, to make the explanation easier, like this:

long broadcastSign = ( ~(inputData << 59) ) >> 63;

The result is that broadcastSign contains either all zeros, or all ones. In other words, it has the sign bit broadcast across the entire long word. How does it work? It relies on the special property of the ASCII code for the minus sign. Its bit number 4 is zero, as opposed to all the digits, where it's one.

To better explain it, let's use some visuals. I'll print the CSV input characters reflected right-to-left, to help you remember they're stored in little-endian order. Here's a temperature reading of -10.8 ℃, with the bit number 4 emphasized in each character:

So, what happens when we perform the bitwise ops as the code says? We'll start with the full long word just like in the picture, with the three missing bytes added on the left:

00000000 00000000 00000000 00111000 00101110 00110000 00110001 00101101

Then shift it left by 59:

inputData << 59 =

01101000 00000000 00000000 00000000 00000000 00000000 00000000 00000000

Our special bit that tells the difference between a digit and the minus sign is now all the way to the left. Let us apply the negation now, flipping all the bits:

~(inputData << 59) =

10010111 11111111 11111111 11111111 11111111 11111111 11111111 11111111

Now the leftmost bit is 1 when the first character is a minus sign, and 0 when it's not a minus sign.

Next, we make an arithmetic shift right by 63. This means that the leftmost bit, as it moves to the right, leaves a "trail" of itself:

broadcastSign = ( ~(inputData << 59) ) >> 63 =

11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111

We end up with the whole long word full of that leftmost bit! If it was 0, the whole word would be zero.

So that's our broadcastSign. It is all ones if there's a minus sign, and all zeros if there's no minus sign. Our example has the minus sign, and therefore it's all ones.

2. Zero out the sign character

Now that we've dealt with the minus sign and stored its information in a variable, we want to get rid of it from the input data. This will make the input data more uniform, and we'll then only deal with the absolute value of the temperature.

It's very easy to zero out the lowest byte in a long number. To do so, just apply the AND mask that has ones all over it, except for the lowest 8 bits. But, the challenge is that this lowest byte may be either a minus sign or a digit, and we must definitely keep the digit intact.

So, we'll construct the AND mask by relying on the broadcastSign variable to guide the calculation towards either all ones (such a mask leaves everything as it was), or the lowest 8 bits set to zero:

long maskToRemoveSign = ~(broadcastSign & 0xFF);
long withSignRemoved = inputData & maskToRemoveSign;

Let's zoom in on the steps now.

broadcastSign =

11111111 11111111 11111111 11111111 11111111 11111111 11111111 11111111

0xFF =

00000000 00000000 00000000 00000000 00000000 00000000 00000000 11111111

broadcastSign & 0xFF =

00000000 00000000 00000000 00000000 00000000 00000000 00000000 11111111

Then we flip all the bits (~), so

maskToRemoveSign = ~(broadcastSign & 0xFF) =

11111111 11111111 11111111 11111111 11111111 11111111 11111111 00000000

This is the case where the minus sign is present. Otherwise, we'd have all zeros in broadcastSign, resulting in all ones in the mask. We got exactly what we wanted.

Now we apply this to inputData, with another AND operation:

withSignRemoved = inputWord & maskToRemoveSign =
00000000 00000000 00000000 00111000 00101110 00110000 00110001 00101101 &
11111111 11111111 11111111 11111111 11111111 11111111 11111111 00000000
=
00000000 00000000 00000000 00111000 00101110 00110000 00110001 00000000

The minus sign is now gone from our inputWord. But if there was a digit instead of the minus sign, it would still be there, untouched.

3. Find where is the decimal dot

We'll find the dot with this statement:

int dotPos = Long.numberOfTrailingZeros(negatedInput & DOT_DETECTOR);

You may have noticed that the dot character . has the same distinguishing property as the minus character: its bit 4 is zero. We'll use that property once again to locate the dot character in the input word. This time we'll apply an AND mask that has 1 at bit 4 of each of the three possible bytes where the dot may appear:

DOT_DETECTOR =
00000000 00000000 00000000 00000000 00010000 00010000 00010000 00000000

Or, in more condensed hexadecimal notation:

DOT_DETECTOR = 0x10101000

Now, since the distinguishing bit is 0 in the dot character, we'll use the negated input word, where this bit will be 1:

negatedWord & DOT_DETECTOR =
11111111 11111111 11111111 11000111 11010001 11001111 11001110 11010010 &
00000000 00000000 00000000 00000000 00010000 00010000 00010000 00000000
=
00000000 00000000 00000000 00000000 00010000 00000000 00000000 00000000

The result is all zero bits except bit number 4 in byte number 3, that is, bit number 3 * 8 + 4 = 28. Now we apply numberOfTrailingZeros to that, and get the number 28. So, for our example of -10.8 ℃, int dotPos = 28.

4. Shift the contents to align to template

Now that we have the position of the dot, we want to shift the contents of the inputWord so that each byte has the same meaning, regardless of the original input format. We want the word to fit into this template:

0 0 0 Z . Y X 0

where:

• X is the tens digit
• Y is the ones digit
• Z is the decimal digit

NOTE: 0 represents a zero byte, not the ASCII character "0"

So far, our word could be in any of these layouts (remember we zeroed out the minus):

0 0 0 Z . Y X 0
0 0 0 0 Z . Y 0
0 0 0 0 Z . Y X
0 0 0 0 0 Z . Y

And we'll use this line of code to align it:

long alignedToTemplate = withSignRemoved << (28 - dotPos)

For our Example 1, with -10.8 ℃, it's easy — the word is already aligned, dotPos = 28, and so we shift by zero.

To see this line of code in action, let's use Example 2, a temperature reading of -7.7 ℃:

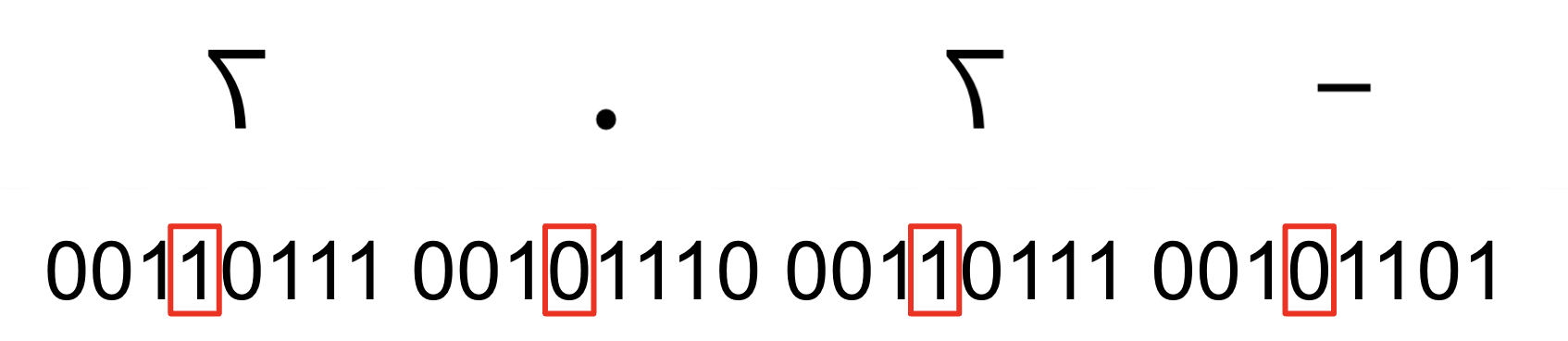
After completing the steps that remove the minus sign, the bytes in the input word will be like this:

0 0 0 0 7 . 7 0

Recall the calculation from the previous step: we apply a mask that ignores the rightmost red rectangle, and isolates the bits in the other three rectangles.

So, it will detect that the 3rd byte from the right has a zero bit in the red rectangle. That's bit number 2 * 8 + 4 = 20. Therefore, dotPos = 20, and since we shift left by 28 - dotPos, we'll shift by 28 - 20 = 8 — one byte to the left.

The result will be this:

0 0 0 7 . 7 0 0

And here's our template once again:

0 0 0 Z . Y X 0

X comes out as 0, exactly as it should be. Our number -7.7 ℃ is equal to -07.7 ℃ — the tens digit is indeed zero.

This step already feels a bit magical. With nothing but straight-through bit manipulation, we managed to align all the different cases to the same fixed template!

5. Transform the ASCII characters to their digit values

From this point on, we return to Example 1: -10.8 ℃.

So far we've been a bit loose in our notation — we used 0 to represent the zero-valued byte, but all the other digits represented ASCII characters. At this point we have to clean this up, because we are after the numerical value of the temperature.

It turns out that the designers of the ASCII table were very careful about this and made it super-simple to go from the digit to the number! As we can see in this excerpt:

         HEX ASCII
          30     0
          31     1
          32     2
          33     3
          34     4
          35     5
          36     6
          37     7
          38     8
          39     9

So all we have to do is zero out the left hex digit (3), and we have the numbers. Since a hex digit corresponds to exactly four bits, this will be easy.

Given our template, the ASCII_TO_DIGIT_MASK constant should now make sense:

0 0 0 Z . Y X 0   <--- template
000000F000F0F00   <--- ASCII_TO_DIGIT_MASK

There are Fs under each of the three digits. Let's go back to our example 1, -10.8 ℃, and set the value of alignedToTemplate against this mask (excuse my one last misuse of 0 to mean both zero and ASCII "0"):

digits = alignedToTemplate & ASCII_TO_DIGIT_MASK =
0 0 0 8 . 0 1 0  &
0 0 0 F 0 F F 0  =

00000000 00000000 00000000 00111000 00101110 00110000 00110001 00000000 &
00000000 00000000 00000000 00001111 00000000 00001111 00001111 00000000 =
00000000 00000000 00000000 00001000 00000000 00000000 00000001 00000000

= 0 0 0 8 0 0 1 0   <--- digits
  0 0 0 Z . Y X 0   <--- template

Matching this to our template, we can see that this exactly represents our number 10.8.

6. Multiply each digit with its weight, and add them all up

And now, for the truly epic grand finale! We'll find a single integer that multiplies our digits number, and somehow magically the temperature value will materialize in the middle of the resulting integer!

To get there, we'll rely heavily on the fact that multiplication and addition are linear operations, and can be decomposed into independent parts that combine into the final result.

First, let's see how we could arrange a multiplier that would make the sum X + Y + Z appear within the result. To do so, we'll evaluate a schematic representation of our digits number. In this representation, each symbol represents four bits, and . represents 0000:

digits = .......Z...Y.X..

We can shift it left by 16 and 24 to align X, Y, and Z within the same bit range:

digits       = .......Z...Y.X..
digits << 16 = ...Z...Y.X......
digits << 24 = .Z...Y.X........
                      ^--------- X, Y, and Z line up here

Now we can sum up these three:

.......Z...Y.X.. +
...Z...Y.X...... +
.Z...Y.X........ =
.Z.Z.YWW.X.Y.X..

Here W stands for X + Y + Z, and is at most 5 bits wide because the sum of three decimal digits is at most 27. Now we can shift this number to the right and apply an AND mask to eliminate what we don't need:

.Z.Z.YWW.X.Y.X.. >> 32 =
.........Z.Z.YWW

.........Z.Z.YWW & 0x1F =
..............WW = X + Y + Z

Bam, out comes our sum!

Now, we could do exactly as described: use two more variables to hold the two shifted numbers, and then sum them up. However, there's a much simpler and cleaner way to represent this. We just need to remember how multiplication works. It's nothing but a sequence of shift-left and add operations! Like this:

X * 00000010 = X << 1
X * 00000110 = (X << 2) + (X << 1)
etc.

So, what is the factor that will do all of our calculation in one go? We simply need a binary number with all zeros except at positions 0 (no shift), 16, and 24:

0001 0000 0001 0000 0000 0000 0001

Or, in the more condensed HEX representation,

MULTIPLIER = 0x01000100000001
           = 0x1 + 0x10000 + 0x1000000

Now we can perform that single multiplication, and get exactly the same effect as we showed above:

.......Z...Y.X.. * (0x1 + 0x10000 + 0x1000000) =
.......Z...Y.X.. +
...Z...Y.X...... +
.Z...Y.X........ =
.Z.Z.YWW.X.Y.X..

This is pretty awesome, but… We don't actually need X + Y + Z, we just used that for practice. We need 100 * X + 10 * Y + Z!

This is where things get really tense. We got assured that our WW part of the result is at most 5 bits wide, representing 27. But, with our actual calculation, this can be a number up to 999, a ten-digit number in binary! And those two WW are right next to Y on the left. Apparently we have room for only 8 bits. Will their bits get mixed together, spoiling our result?

We have to look at this very carefully. Let's use our schematic again, but now we'll add the decimal multipliers 100 and 10 in the right places:

0x.......Z...Y.X.. * (0x1 + 10 * 0x10000 + 100 * 0x1000000) =

0x.......Z...Y.X.. * 1  +
0x...Z...Y.X...... * 10 +
0x.Z...Y.X........ * 100

We can see that the first two rows give us no trouble.

• In the first row, Z is well isolated from the others.
• In the second row, X is tightly below Y, but that row is only multiplied by 10, with the maximum value of 90, occupying 7 bits.
• In the third row, however, we have X * 100, ten bits wide, enroaching on the bit positions of Y. Here, it seems that the scheme may break.

But then, almost as a deus ex machina, we realize that Y is also multiplied by 100, which breaks down into 4 * 25 — that 4 in there is a round binary number 100.

Just like multiplying by decimal 100 results in a decimal number ending in two zeros, so does multiplying by binary 100 result in a binary number ending with two zeros. The rightmost two bits of Y * 100 will therefore be zero, and that is exactly the two bits that we need to fit X * 100!

So we escape by a split hair and get a clean sum of all three rows in the bit range 41..32. As merykitty commented, // That was close :)

Let's wrap up this step with the complete formula:

MAGIC_MULTIPLIER = 0x1 + 10 * 0x10000 + 100 * 0x1000000
absValue = ((digits * MAGIC_MULTIPLIER) >>> 32) & 0x3FF

0x3FF is a number with ten ones in binary form, isolating our ten-bit-wide result.

7. Apply the sign

After all the fireworks in the previous step, this step is kind of an anticlimax. And yet, even here we find ingenious tricks.

So far, we have the absolute value of the temperature (multiplied by 10 so that it's an integer), and, in a separate variable, we have the information whether there is a minus sign. This is encoded in the variable broadcastSign as 0 for "no minus", and -1 for "yes minus".

How do you put the sign on the absolute value, without using an if? If the "no minus" case was encoded as 1, it would be a trivial multiplication. But, that's just wishful thinking, we have what we have. We're so close, is there anything else we can use? One last magic trick?

Yes, there is a trick! It's a very well-known, basic concept, but coming to realize it's the right thing in this moment was a touch of genius.

There's a good chance you already know how signed integers work in programming languages. We don't just slap on a sign bit to signal a negative number. We use the two's complement formula:

-n = NOT(n) + 1

Now look and marvel how this formula serves us the solution on a silver platter. We need one of these two things to happen:

1. value = absValue when there is no minus sign

OR

2. value = NOT(absValue) + 1 when there is a minus sign.

We can call upon the XOR operation to act as switchable negation: n XOR -1 is NOT(n), and n XOR 0 is just n. Guess what, this is an exact match to the value of broadcastSign! As for our optional + 1, we can conveniently use -broadcastSign. So, our formula is this:

temperature = (absValue ^ broadcastSign) - broadcastSign

And there it is, our temperature has materialized!

8. Bonus: compute the end of the CSV row

Now that we have the temperature, you may wonder why go on. In the broader 1BRC solution, it was very important to also cheaply find out where the next CSV line starts.

We calculate that by using the decimal dot as the anchor, because after it there's always one decimal, followed by a newline. dotPos, as you recall, is the number of bits, not bytes, so we divide it by 8 (shift right by 3, same thing) and add three, in order to point out the first byte of the next CSV line:

nextLineStart = (dotPos >>> 3) + 3

Conclusion

While I can hope this blog post explained the mystery behind merykitty's magic SWAR, the real mystery is how a single guy working alone could come up with all this in just a few days of casually doing an online challenge with a T-shirt and a coffee mug as a reward.

That is the kind of mystery you won't find a blog post explaining.

Take care!