In the world of databases, benchmarking performance has always been the hottest topic. Who is faster for data ingestion and queries? About a month ago we announced a new release with SIMD aggregations on HackerNews and Reddit. Fast. But were those results numerically accurate?
Speed is not everything. Some of the feedback we have received pointed us toward the accuracy of our results. This is something typically overlooked in the space, but our sums turned out to be "naive", with small errors for large computations. By compounding a very small error over and over through a set of operations, it can eventually become significant enough for people to start worrying about it.
We then went on to include an accurate summation algorithm (such as "Kahan" and "Neumaier" compensated sums). Now that we're doing the sums accurately, we wanted to see how it affected performance. There is typically a trade-off between speed and accuracy. However, by extracting even more performance out of QuestDB (see below for how we did it), we managed to compute accurate sums as fast as naive ones! Since comparisons to Clickhouse have been our most frequent question, we have run the numbers and the result is: 2x faster for summing 1bn doubles will nulls.
All of this is included in our new release 4.2.1
You can find our repository on GitHub. All your issues, pull-requests and stars are welcome 🙂.
How did we get there?
We used prefetch and co-routines techniques to pull data from RAM to cache in parallel with other CPU instructions. Our performance was previously limited by memory bandwidth - using these techniques would address this and allow us to compute accurate sums as fast as naive sums.
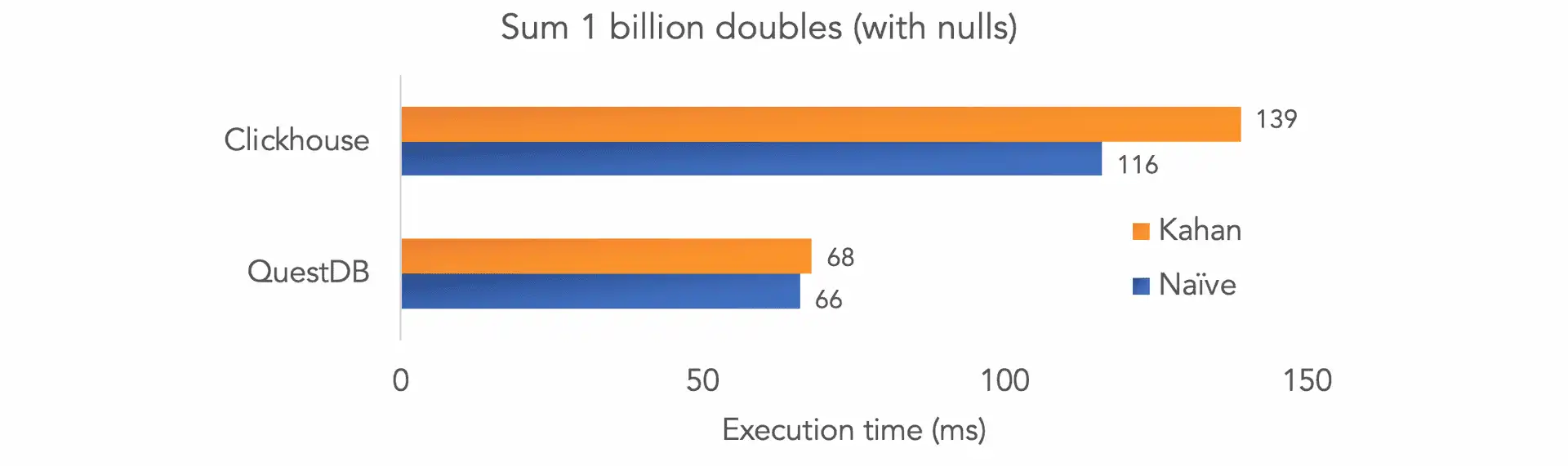
With the help of prefetch we implemented the fastest and most accurate summation we have ever tested - 68ms over 1bn double values with nulls (versus 139ms for Clickhouse). We believe this is a significant advance in terms of performance for accurate summations, and will help developers handling intensive computations with large datasets.
Contents
- An introductory example of the problem with summing doubles.
- A quick glance at floating points inaccuracies.
- A presentation of the Kahan algorithm.
- Our compensated sum implementation using SIMD instructions.
- A benchmark versus Clickhouse for naive and accurate summation methods.
How inaccurate floating-point operations occur
Before we dig in, some of you might wonder how an addition can be inaccurate as opposed to simply right or wrong.
CPUs are poor at dealing with floating-point values. Arithmetics are almost
always wrong, with a worst-case error proportional to the number of operations
n. As floating-point operations are intransitive, the order in which you
perform them also has an impact on accuracy.
Here is an example:
public static void main(String[] args) {
System.out.println(5.1+9.2);
}
We ask to add 5.1 to 9.2. The result should be 14.3, but we get the
following instead.
14.299999999999999
It is a small difference (only 0.000000000000001), but it is still wrong. To
make matters worse, this error can be compounded.
public static void main(String[] args) {
double a = 5.1+9.2;
double b = a + 3.5;
double c = 14.3 + 3.5;
System.out.println("The result is: " + b);
System.out.print("But we expected: " + c);
}
The result is: 17.799999999999997
But we expected: 17.8
The error has just grown to 0.000000000000003 and will keep on growing as we
add operations.
Float representation and truncation accuracy loss
Decimal numbers are not accurately stored. This is well documented already, for example on StackOverlow or 0.30000000000000004.com.
Consequently, operations on floating points will return inaccurate results. This is not the only problem. Performing operations is also likely to introduce more errors and to grow the total error over time. One such case is once the result of an operation has to be truncated to fit the original format. Here is a simplified example of the truncation that happens when adding floats of different orders of magnitude.
For the below example we will be using base 10 and expressing the exponent as a number rather than a binary for sake of simplicity. We assume 5 significant digits.
We start with both our numbers expressed in scientific notation.
Let's expand into decimal notation and place them on a similar scale so all digits fit.
Now, let us express this sum back as one number in scientific notation. We have
to truncate the result back to 5 significant digits.
The result is incorrect. In fact, it is as if we did not sum anything.
Kahan's algorithm for compensated summation
Compensated sum maintains a sum of accumulated errors and uses it to attempt to correct the (inaccurate) sum by the total error amount. It does so by trying to adjust each new number by the total accumulated error.
The main Compensated summation algorithm is the Kahan sum. It runs in 4 steps:
- Subtract the
running errorfrom the newnumberto get theadjusted number. If this is the first number, then the running error is 0. - Add the
adjusted numberto therunning totaland truncate to the number of significant digits. This is thetruncated result. - Calculate the
new running erroras(truncated result - running total) - adjusted number. - Assign the
truncated resultas the newrunning total.
This works because of addition transitivity rules.
Kahan implementation with SIMD instructions
Now, the interesting bit! QuestDB implements the same 4-step algorithm as Kahan. However, it uses vectorized instructions to make things a lot faster. The idea came from Zach Bjornson who wrote about this on his blog.
Here is our implementation in details:
We first define our vectors:
Vec8d inputVec;
const int step = 8;
const auto *lim = d + count;
const auto remainder = (int32_t) (count - (count / step) * step);
const auto *lim_vec = lim - remainder;
Vec8d sumVec = 0.;
Vec8d yVec;
Vec8d cVec = 0.;
Vec8db bVec;
Vec8q nancount = 0;
Vec8d tVec;
Then we load vectors with data. What's happening below is exactly Kahan's algorithm. However, instead of summing individual values, we are summing vectors of 8 values each.
for (; d < lim_vec; d += step) {
_mm_prefetch(d + 63 * step, _MM_HINT_T1);
inputVec.load(d);
bVec = is_nan(inputVec);
nancount = if_add(bVec, nancount, 1);
yVec = select(bVec, 0, inputVec - cVec);
tVec = sumVec + yVec;
cVec = (tVec - sumVec) - yVec;
sumVec = tVec;
}
The strategically placed prefetch relies on CPU pipelining. The goal is to
have the CPU fetching the next chunk of data from RAM to cache while we are
calculating the current vector.
Lastly, we use horizontal_add to sum all values into a scalar value. Again, we
recognise Kahan's sum algorithm.
double sum = horizontal_add(sumVec);
double c = horizontal_add(cVec);
int nans = horizontal_add(nancount);
for (; d < lim; d++) {
double x = *d;
if (x == x) {
auto y = x - c;
auto t = sum + y;
c = (t - sum) -y;
sum = t;
} else {
nans++;
}
}
Comparing performance versus ClickHouse
We compared how performance behaves when switching from naive (inaccurate) sum to Kahan compensated sum.
Hardware
We run all databases on an c5.metal AWS instance, which has two Intel 8275CL
24-core CPUs and 192GB of memory. QuestDB was running on 16 threads. As we
showed in a
previous article,
adding more threads does not improve performance beyond a certain point.
Clickhouse was running using all cores as per default configuration, however we
increased the memory limit from the default value from 10GB to 40GB
<max_memory_usage>40000000000</max_memory_usage>.
Test data
We generated two test files using our random generation functions and exported the results to CSV. We then imported the CSV individually in the databases.
SELECT rnd_double() FROM long_sequence(1_000_000_000l); -- non null
SELECT rnd_double(2) FROM long_sequence(1_000_000_000l); -- with nulls
Storage engine
- QuestDB: on disk
- Clickhouse: in memory (using the
memory()engine)
Commands
With null
| Description | QuestDB | Clickhouse |
|---|---|---|
| DDL | CREATE TABLE test_double AS(SELECT rnd_double() FROM long_sequence(1000000000L); | CREATE TABLE test_double (val Nullable(Float64)) Engine=Memory; |
| Import | Not required | clickhouse-client --query="INSERT INTO test_double FORMAT CSVWithNames;" < test_double.csv |
| Naive sum | SELECT sum(val) FROM test_double; | SELECT sum(val) FROM test_double; |
| Kahan sum | SELECT ksum(val) FROM test_double; | SELECT sumKahan(val) FROM test_double; |
Non-null
For non-null values, we adjusted the commands as follows:
- use
test_double_not_nul.csvinstead oftest_double.csv. - for Clickhouse, skip declaring val as
nullable:CREATE TABLE test_double_not_null (val Float64) Engine=Memory;. - for QuestDB, replace
rnd_double()byrnd_double(2)at the DDL step.
Results
We ran each query several times for both QuestDB and Clickhouse and kept the best result.
Without null values, both databases sum naively at roughly the same speed. With Kahan summation, QuestDB performs at the same speed while Clickhouse's performance drops by ~40%.
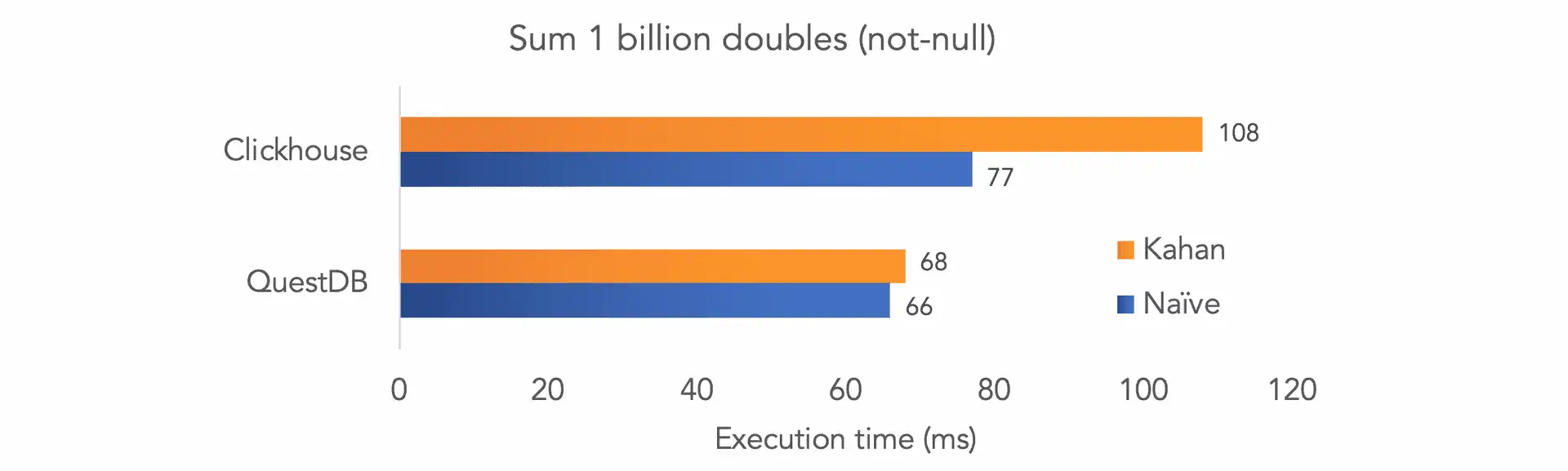
As we include null values, Clickhouse's performance degrades by 28% and 50% for naive and Kahan summation, respectively.
What we learned
It is useful to stabilize aggregation with compensated sums. We learned that vector-based calculation produce different arithmetic errors compared to non-vector calculations. The way the aggregation is executed by multiple threads is not constant. This can cause results to be different from one SQL run to another, if the sum is accuracy naive. Through compensated sums, the results are consistent and more accurate.
It was also both interesting and surprising to be able to quantify the effect of prefetch on what is essentially sequential memory read.
Your support means a lot to us! If you like content like this, what we do, and where we're going, please join our community forums and give us a star️ on GitHub.